الرياضيات: الدوائر والمحيط للصف العاشر عام ( المنهج الإماراتي )

سنتعرف في هذا الدرس من دروس الرياضيات على أهم المفاهيم الأساسية في الدائرة، تعريفها، نصف قطرها، قطرها،الوتر ، علاقات نصف القطر والقطر، وعلاقاتي المحيط.

تعريف الدائرة: الدائرة هي المحل الهندسي لمجموعة من جميع نقاط المستوي متساوية البعد عن نقطة ثابتة تدعى مركز الدائرة للقطع التي تقطع دائرة أسماءها خاصة.

المفهوم الرئيسي القطع الخاصة في دائرة

نصف القطر: هو قطعة مستقيمة تقع إحدى نقطتاها الطرفيتان في المركز والأخرى على الدائرة.

أمثلة: حدد أنصاف الأقطار في الدائرة الآتية:

 

 

 

 

 

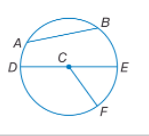
أنصاف الأقطار هي: CE  ،  CE   ،  CD

وهي أنصاف أقطار لأنها قطعة مستقيمة إحدى نقاطها هي مركز الدائرة والنقطة الأخرى تقع على الدائرة

الوتر: قطعة مستقيمة تقع نقطتاها الطرفيتان على الدائرة.
أمثلة: حدد الأوتار في الدائرة السابقة

AB ، DE

وهي أوتار لأنها عبارة عن قطعة مستقيمة نقطتاها الطرفيتان تقع على الدائرة

القطر: في دائرة هو وتر يمر من المركز ويتكون من نصفي قطرين يقعان على استقامة واحدة.
مثال:  في الدائرة السابقة إن DE هو قطر يتكون من نصفي القطرين: CD ، CE الواقعين على استقامة واحدة

أمثلة تحديد القطع في دائرة:

مثال 1:

لدينا الدائرة الآتية سمها وحدد انصاف الأقطار بها

 

 

 

 

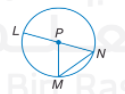
الحل: يقع مركز الدائرة عند النقطة P ،ولذلك تسمى بالدائرة P

أنصاف الأقطار هي: PN ،  PM ،  PL

وذلك لأنها عبارة عن قطع مستقيمة إحدى نقاطها مركز الدائرة والنقطة الأخرى تقع على الدائرة

مثال 2:

لدينا الدائرة الآتية حدد وتراً وقطراً بها

 

 

 

 

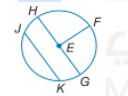
الحل:

بحسب تعريف الوتر:هو  قطعة مستقيمة تقع نقطتاها الطرفيتان على الدائرة.

فإنّ JK هو وتراً في الدائرة

وبحسب تعريف القطر: في دائرة هو وتر يمر من المركز ويتكون من نصفي قطرين يقعان على استقامة واحدة.

فإنّ HJ هو القطر في الدائرة

ملاحظة هامة: بما أن المسافة من مركز الدائرة إلى أي نقطة من محيطها هي واحدة دائماً فإنّ جميع أنصاف الأقطار في الدائرة نفسها متطابقة.

وبما أنّ القطر يتركب من نصفي قطرين فإنّ جميع أقطار الدائرة متطابقة أيضاً.

المفهوم الأساسي علاقات نصف القطر والقطر:

إذا كان لدائرة نصف القطر الذي يرمّز ب r والقطر الذي يرمّز ب d فإنّ العلاقات الآتية تنطبق عليها:

 

 

وهي تعني : ن طول نصف القطر يساوي نصف طول القطر

وأنّ طول القطر يساوي ضعفي طول نصف القطر

مثال إيجاد نصف القطر والقطر:

إذا كان طول  QV=8 cm فما قطر الدائرة Q ؟

الحل:

بما أنه معلوم لدينا في نص المسألة طول نصف القطر فنكتب قانون قطر الدائرة الذي ذكرناه آنفاً وهو:                                     d=2r

ثمّ نعوّض طول نصف القطر بالقانون فنجد:

d=2(8)=16 cm

 

المفهوم الأساسي انصاف الدوائر:

1. تتطابق دائرتان حصرا إذا كانتا تضمان نصفي قطرٍ متطابقين.

مثال عن دائرتين متطابقتين:

 

 

 

 

 

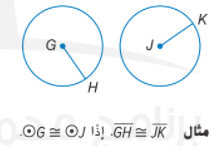
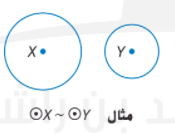
2. كل الدوائر متشابهة

مثال عن دائرتين متشابهتين:

 

 

 

 

 

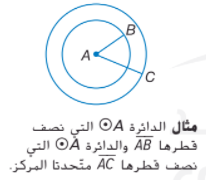
3. الدوائر متحدة المركز هي دوائر متّحدة المستوى لها المركز نفسه.

مثال عن دوائر متحدة المركز:

 

 

 

 

 

 

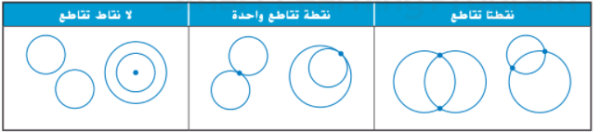
الدوائر المتقاطعة:

يمكن لدائرتين أن تتقاطعا في نقطة واحدة ، ويمكن أن تتقاطعا في نقطتين مختلفتين ، ويمكن ألاّ تتقاطعا بأي نقطة.

وسنعطي أمثلة على ذلك من خلال الرسم:

 

 

 

 

 

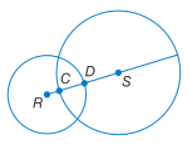
مثال عن إيجاد قياسات في الدوائر المتقاطعة:

قطر الدائرة S ⊙يساوي 30 وحدة، وقطر الدائرة R يساوي 20 وحدة، وحدة 9 = DS .جـد CD.

 

 

 

 

 

الحل:

نلاحظ أن الدائرتين متقاطعتين في نقطتين مختلفتين

وقطر الدائرة S يساوي 30 إذاً:

CS=15 لأنه نصف قطر ( حسب قانون نصف القطر الذي تعلمناه سابقاً)

و إنّ DS=9 ومنه نستنتج طول CD من خلال العلاقة الآتية: (مسلمة جمع القطع المستقيمة)

CD+DS=CS

نعوّض بالأعداد المعلومة لدينا:

CD+9=15

نطرح 9 من كل طرف من طرفي المعادلة فنحصل على النتيجة المطلوبة:

CD=6

المحيط:

محيط الدائرة هو المسافة حول الدائرة. وبالتعريف، فإن النسبة C/d  هي عدد غير نسبي
يدعى باي ، ويمكن اشتقاق قانونين لحساب المحيط عبر استخدام التعريف

شرح التعاريف:

إذا كان لدائرة القطر d ونصف القطر r ،فإن المحيط C يساوي القطر مضروب بالعدد باي.

أو مثلي نصف القطر مضروباً بالعدد باي.

مثال على إيجاد المحيط:

في عام 2005 ،لعب روجيه فيدرير وأندريه أغاسي على منصة هبوط الطائرات الحوامة في برج
العرب بالإمارات العربية المتحدة. وكان قطر منصة الهبوط يساوي 24 متراً وارتفاعها قرابة 213 متراً .

والمطلوب: جـد محيط منصة هبوط الطائرات الموصوفة.

الحل: بما أن قطر منصة الهبوط معلوم ويساوي 24 متراً لذا نستطيع تطبيق قانون محيط الدائرة الذي يحوي على القطر وهو:

ثمّ نعوّض d بالعدد 24 فنجد:

وباستخدام الآلة الحاسبة نجد أن المحيط يساوي تقريباً

   C=75.4