تعلّم معنا درس: مجموعة الأعداد

مجموعة الأعداد الطبيعية ورمزها ( N ):

وتتضمن الأعداد:

. . . . . . . . . . .. . .,0,1,2,3,4,5

مجموعة الأعداد الصحيحة ورمزها (Z ):

وتتضمن الأعداد الموجبة والسالبة والصفر أي:

. . . . . . , -4,-3,-2,-1,  0 ,+1,+2,+3,+4, . . . . . . . . .

أي أنها تحتوي على الأعداد الطبيعية بالإضافة إلى الأعداد الصحيحة السالبة , وبالتالي فإن مجموعة الأعداد الطبيعية محتواة في مجموعة الأعداد الصحيحة.

مجموعة الأعداد العشرية ورمزها ( D):

 

تعريف العدد العشري :

هو أي عدد نستطيع كتابته بالشكل:

حيث أن : P عدد صحيح , N عدد طبيعي

ولسهولة الفهم نحفظ أن الأعداد العشرية هي الأعداد التي تحتوي على فاصلة عشرية .

أمثلة على الأعداد العشرية:

3,5  ،   1,5-     ,    13,7-

مثال تطبيقي:

هل العدد:

عشري أم غير عشري ؟

الحل:

حتى نستطيع أن نحدد هل هذا الكسر عشري أم غير عشري علينا أن نقسم البسط على المقام وهناك حالتين :

إن كان الناتج هو عدد منتهي أي أن باقي القسمة صفراً فيكون الكسر عشري

وإن كان الناتج هو عدد غير منتهي ودوري ( سنوضح ذلك بمثال لاحق) فيكون العدد غير عشري ودوري

نلاحظ في هذا المثال أن ناتج القسمة هو العدد 2,5 وهو عدد منهي لأن باقي عملية قسمة العدد 5/2 هو الصفر ، وبالتالي فإن العدد 5/2 هو عدد عشري .

مجموعة الأعداد العادية ورمزها ( Q ) :

وهي مجموعة تحتوي على جميع الأعداد الموجودة في المجموعات السابقة بالإضافة إلى الكسور أي تحتوي على :

الأعداد الموجبة والسالبة والصفر والأعداد العشرية بالإضافة إلى الكسور

 

أمثلة على الأعداد العادية:

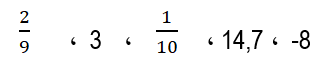
مجموعة الأعداد الحقيقية أو غير العادية ورمزها ( R ):

وهي المجموعة التي تحتوي على جميع الأعداد السابقة بالإضافة إلى الجذور والعدد

 

أمثلة على الأعداد الحقيقية:

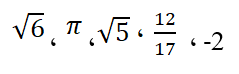
تمارين:

عين طبيعة كلاً من الأعداد الآتية:

التمرين الأول:

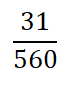
الحل:

علينا هنا معرفة أصغر مجموعة يحتوي بها هذا العدد ،  ولهذا نقوم بقسمة البسط على المقام حتى نستطيع تحديد إن كان العدد عشري أو عادي

بإجراء عملية القسمة ( شرح القسمة في الفيديو المرفق في نهاية المقال )

تكون الإجابة :

0,0375     = 21/560

والباقي يساوي صفر

أي أن الكسر عشري لأنه منتهي ، ينتج أن العدد عشري

 

التمرين الثاني:

الحل:

بنفس طريقة التمرين السابق نقسم البسط على المقام فتكون الإجابة :

…..1،666666 =5/6

ونلاحظ في هذا التمرين أن العدد 6 مكرر عدد لانهائي من المرات ، بالتالي فإن العدد غير عشري ودوري ، لذا فإنه لاينتمي إلى مجموعة الأعداد العشرية بل إلى مجموعة الأعداد العادية Q .

لمزيد من الأمثلة والشرح المفصّل شاهدوا هذا الفيديو: