التابع الزوجي والتابع الفردي
سنتعرف في هذا المقال على الشروط التي يجب تحققها حتى يكون التابع زوجي أو فردي ، وسنتعرف على الشكل الذي يكون عليه الخط البياني للتابع الزوجي والتابع الفردي ، وبالعكس أي سنتعلم معرفة هل التابع فردي أم زوجي من شكل الخط البياني لهذا التابع .
شروط التابع الزوجي:
حتى يكون أي تابع هو تابع زوجي يجب تحقق الشرطين الآتيّن:
![]()
![]()
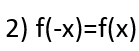
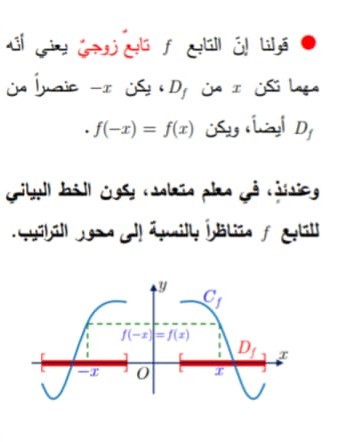
وعندئذ في معلم متعامد ، يكون الخط البياني للتابع متناظراً بالنسبة إلى محور التراتيب ، كما بالشكل الآتي:
شروط التابع الفردي:
حتى يكون أي تابع هو تابع فردي يجب تحقق الشرطين اللآتيّن:
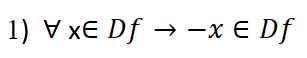
![]()
![]()
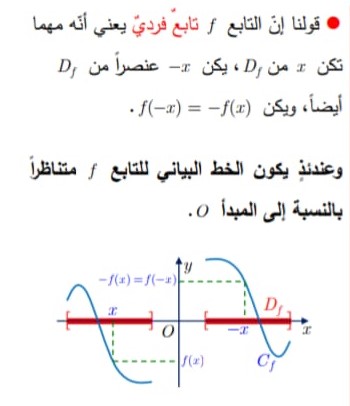
وعندئذ في معلم متعامد ، يكون الخط البياني للتابع متناظراً بالنسبة إلى المبدأ O.
كما بالشكل الآتي:
أمثلة:
بيّن أي من التوابع الآتية تابع زوجي ، وأي منها تابع فردي:
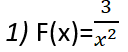
لنتحقق أولًا من شروط زوجية التابع ، نكتب الشرط الأول:
![]()
![]()
التابع هنا هو تابع كسري مجموعة تعريفه هي:
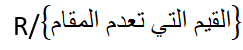

فإن القيم التي تعدم المقام هي الصفر
إذاً فمجموعة تعريف التابع هي:
![]()
نعود للشرط الأول ونتأكد من تحققه:
![]()
نلاحظ أن الشرط محقق لأنه إن قمنا بتجريب أي عدد ينتمي إلى مجموعة الأعداد الحقيقة ماعدا العدد صفر ولنأخذ مثال العدد 3 فنلاحظ أن معاكس العدد وهو بالمثال 3- ينتمي إلى مجموعة الأعداد الحقيقية ماعدا الصفر .
لنتأكد من تحقق الشرط الثاني من شروط زوجية التابع:
![]()

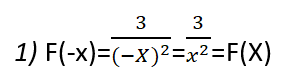
وهو الشرط الثاني من شروط التابع الزوجي وبالتالي فالتابع زوجي.
مثال2:
![]()
مجموعة تعريف التابع هي R لنتأكد من تحقق الشرط الأول :
![]()
لنتأكد من تحقق الشرط الثاني للتابع الفردي مثلاً:
![]()
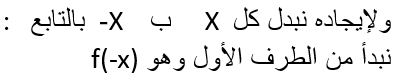
![]()
ونلاحظ أنه لايساوي f(x) – ولا يساوي F(x) وبالتالي فالتابع ليس تابعًا زوجيًّا وليس تابعًا فرديًّا.
لمزيد من الأمثلة شاهدوا الفيديو الآتي:

