التابع الصحيح (كثير الحدود)

سنتعرف في هذا المقال على شكل التابع الصحيح أو مايعرف بالتابع كثير الحدود، وعلى مجموعة تعريفه ، ونهايته عند الزائد لانهاية وعند الناقص لانهاية وعند عدد ما.

 أولاً: شكله العام:

حيث:

a,b,…..,K أعداد حقيقية

 عدد طبيعي n

أمثلة على بعض التوابع الصحيحة:

تابع صحيح من الدرجة الثانية

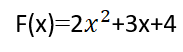
تابع صحيح من الدرجة الأولى

ثانياً: مجموعة تعريفه:

مجموعة تعريفه هي مجموعة R  (وهي مجموعة الأعداد الحقيقية)

 

ثالثاً: (نهاية التابع الصحيح)

 

لدينا حالتان:

 

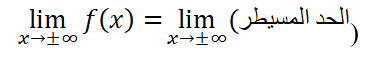
الحد المسيطر هو الحد الذي يمتلك أعلى أس في كثير الحدود              

أمثلة:

– أوجد نهاية كلٍ من التوابع الآتية عند الزائد لانهاية وعند الناقص لانهاية

الحل:

 

الحد المسيطر وأمثاله هو :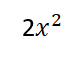

ومنه فإن الحل يكون بالشكل الآتي:

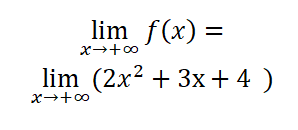
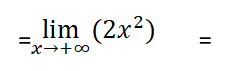
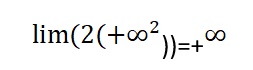
” بدلنا كل x بالزائد لانهاية”

وبنفس الطريقة نوجد نهاية التابع عندما  x تسعى نحو الناقص لانهاية

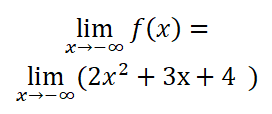
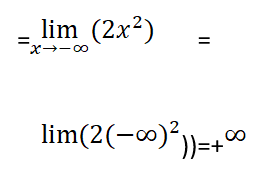
الحالة الثانية:( عندما تسعى x نحو عدد ) 

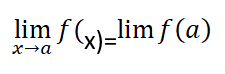
أي نبدل كل x ب a بالتابع المعطى

 

مثال:

أوجد نهاية التابع:

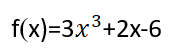
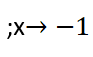
الحل:

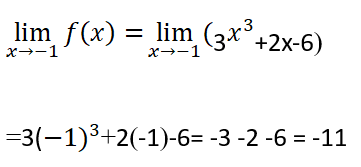
ولمزيد من الفائدة تابعوا هذا الفديدو: