تمثيل المعادلات بيانياً بصيغة الميل والمقطع (المنهج الإماراتي):

سنتعلم في هذا الدرس من دروس الرياضيات ماذا يقصد بتمثيل المعادلات بيانياً ، وماهي الصيغة العامة للمعادلة بصيغة الميل والمقطع، وكيف نستطيع تمثيل المعادلات بيانيًا بصيغة الميل والمقطع وذلك من خلال الأمثلة التوضيحية.

أولاً مالمقصود بتمثيل المعادلات بيانياً:

يقصد بتمثيل المعادلات بيانياً أي تمثيل المعادلة في المستوي الاحداثي ،

Oxy ذو المحوريين الاحداثيين Ox ، oy المتعامدين والمرقيمين كما في الشكل:

ثانياً صيغة الميل والمقطع:

إنّ الشكل العام لصيغة الميل والمقطع هي:

Y=mx+b

حيث إنّ: M هي الميل و b هي نقطة التقاطع مع المحور الرأسي Oy

وتسمى أيضاً معاملات المعادلة ، حيث أنها تتغير بتغير المعادلة.

مثال:

Y=2x+6

الميل هنا هو أمثال المتحول X و b=6 وهي نقطة التقاطع مع المحور الرأسي

ثالثاً تمثيل المعادلات بيانياً بصيغة الميل والمقطع:

اكتب المعادلة بصيغة الميل والمقطع للخط ذي الميل بقيمة 4/3

ونقطة التقاطع مع المحور الرأسي بقيمة 2- ، ثم مثل المعادلة بيانياً.

•  نكتب الصيغة العامة للمعادلة ثم نعوض بالمعطيات المعطاة:

Y=mx+b

Y=3/4x-2

•  تمثيل المعادلة بيانياً:

نرسم المستوي الاحداثي والذي هو عبارة عن المحوريين المتعامدين

Ox،oy

ونرقمهما كما في الشكل السابق:

 

 

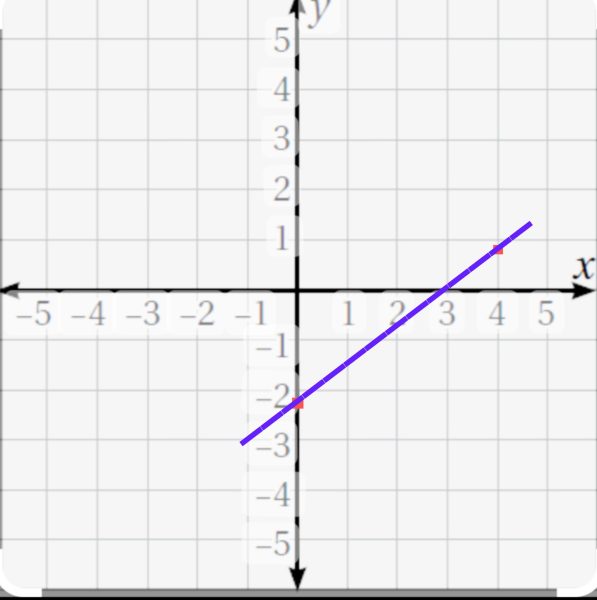
نعين نقطة التقاطع مع المحور الرأسي ، وهي نقطة فاصلتها دائماً صفر وترتيبها هو النقطة B المعطاة أي هي 2-

فتصبح احداثيات النقطة هي:

(2-، 0)

• ثمّ نعينها في المستوي الاحداثي.
• نستفيد من الميل المعطى في نص المسألة بالشكل:

4/ 3= التغير الأفقي/التغير الرأسي

من النقطة  (2-، 0)

• نحرك 3 وحدات إلى الأعلى (حسب التغير الرأسي)

ثمّ نحرك أربع وحدات نحو اليمين ( حسب التغير الأفقي)

• ونعين النقطة وتكون هي النقطة (1 ، 4).
• نصل بين النقطتين  (2-، 0)و (1 ، 4).

فنحصل على المستقيم المطلوب كما في الشكل الآتي:

 

للمزيد من الشرح المفصل والتوضيحي شاهدوا الفيديو الآتي: