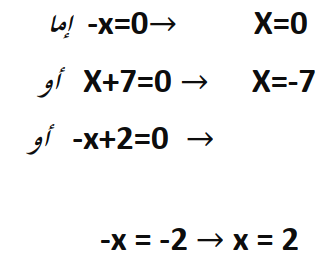حل المعادلات…باستخدام خاصية الجداء الصفري
حل المعادلات… باستخدام خاصة الجداء الصفري
لنتعلم أولا متى نستخدم هذه الخاصة وماذا يقصد بالجداء الصفري .
نستخدمها في حل المعادلات من الدرجة الثانية فأكثر ، أي من الدرجة الثانية والثالثة والرابعة و … الخ
وعندما يكون لدينا جداء عدة حدود جبرية تساوي الصفر ويجب أن تساوي الصفر حصرا ولهذا سميت بالجداء الصفري .
لنأخذ أمثلة ونتعلم كيف نحلها :
أمثلة :
فكرة الحل هي أنه حتى يكون جداء حدين يساوي الصفر يجب أن يكون أحدهما على الأقل يساوي الصفر ، أي يجب أن يكون إما القوس الأول يساوي الصفر أو القوس الثاني يساوي الصفر أو القوس الثاني يساوي الصفر ، ونلاحظ أن كلها القوسين يحتويان على مجهول من الدرجة الأولى ، فنحصل عند مساواة القوس بالصفر على معادلة من الدرجة الأولى تحل ببساطة .
الحل:
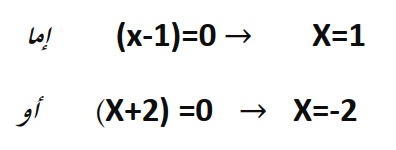
بنفس طريقة الحل السابقة نحل هذا التمرين
الحل:
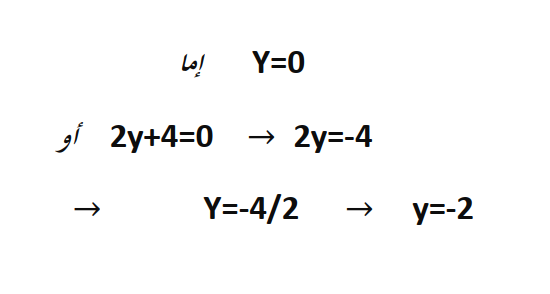
الحل :
نلاحظ في هذا التمرين جداء ثلاثة حدود يساوي الصفر ،فيكون حله إما الحد الأول يساوي الصفر ، أو الحد الثاني يساوي الصفر ،أو الحد الثالث يساوي الصفر
