دراسة جهة الاطراد لمجموع تابعين
سنتعرف في هذا المجال على مفهوم جهة الاطراد ، وسندرس جهة الاطراد لمجموع تابعين مع مثال تطبيقي لتكريس الفهم.
مفهوم جهة الاطراد:
يقصد بجهة الاطراد أي هل التابع متزايد تماماً، متناقص تماماً، متزايد أو متناقص.
مبرهنة:
- مجموع تابعين متزايدين تماماً على مجال ما هو تابع متزايد تماماً على نفس المجال.
- مجموع تابعين متناقصين تماماً على مجال ما هو تابع متناقص تماماً على نفس المجال.
مثال:
لدينا التابعين F(x) ,g(x) المعرفين على المجال:
حيث أن:
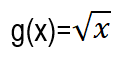
هل التابع F+g متزايد تماماً ؟
الحل:
لمعرفة فيما إذا كان التابع f+g متزايد تماماً أم لا يجب معرفة جهة الاطراد لكلا التابعين
f,g
لنبدأ بدراسة جهة اطراد F(x) :
يوجد طريقتين لمعرفة جهة اطراد التابع
الطريقة الأولى هي أن التابع f(x) هو من التوابع المرجعية ( التي قمنا بدراستها في الصف العاشر)
التوابع المرجعية مرفقة بالصورة الآتية:
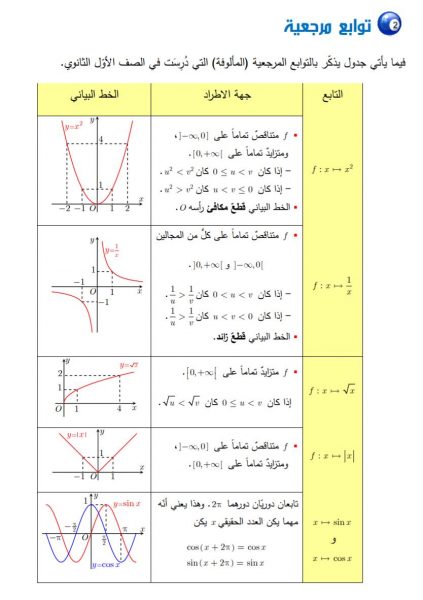
ومنه نستنتج أن التابع f تابع متزايد تماماً على المجال
و نكتفي بكتابة أن التابع f متزايد تماماً على هذا المجال .
الطريقة الثانية باستخدام تعريف التابع المتزايد تماماً والتابع المتناقص تماماً التي قمنا بدراستها أيضاً في الصف العاشر .
تعريف التابع المتزايد تماماً:
وللسهولة نجرب أرقام من المجال المعطى :
أولاً F(X)
لنجرب العددين 1،4 في التابع
من المعروف أن :
يبقى أن نبرهن أن:
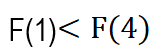
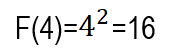
ومنه نستنتج أن:
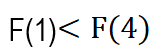
ومنه نستنتج أن التابع f متزايد تماماً على المجال
ثانياً: التابع g(x)
نستطيع بنفس طريقة التعريف إثبات أن التابع g(x) هو تابع متزايد تماماً.
ولكن للسهولة نثبت أن التابع g متزايد تماماً عن طريق تذكر التوابع المرجعية التي ذكرناها في بداية المقال
أي أن التابع (x)g متزايد تماماً على المجال :
ومنه باستخدام المبرهنة: مجموع تابعين متزايدين تماماً هو تابع متزايد تماماً
نستنتج أن تابع المجموع F+g هو تابع متزايد تماماً على المجال
لمزيد من الأمثلة والشرح على هذا الدرس يرجى مشاهدة الفيديو الآتي: