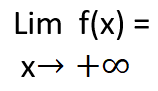قواعد إيجاد نهاية التابع الكسري

سنتعرف في هذا المقال على تعريف التابع الكسري ، وعلى مجموعة تعريف التابع الكسري ، وعلى نهاية التابع الكسري عندما x تسعى نحو الزائد لانهاية أو الناقص لانهاية ، وعندما x تسعى نحو عدد ما.

 

التابع الكسري :

هو تابع يحتوي على بسط ومقام ، شرط أن يحتوي مقامه على متغير (مجهول) من الدرجة الأولى فأكثر .

أمثلة على بعض التوابع الكسرية :

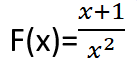
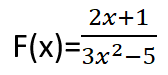
مجموعة تعريف التابع الكسري :

هي مجموعة الأعداد الحقيقية R ماعدا القيم التي تعدم المقام  ونكتبها بالشكل:

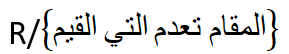
نهاية التابع الكسري :

الحالة الأولى:( عندما x تسعى نحو الزائد لانهاية أو نحو الناقص لانهاية)

هي نهاية ( الحد المسيطر بالبسط/الحد المسيطر بالمقام)

وذلك عندما x تسعى نحو الزائد لانهاية أو نحو الناقص لانهاية.

ونكتبها بالشكل:                                                                                   

 

 

 

 

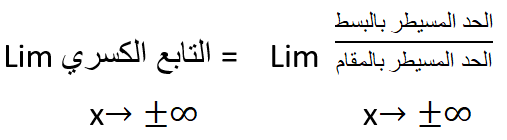
ويقصد بالحد المسيطر أي المجهول (المتجول) الذي يملك أعلى درجة من الأس .  

 

الحالة الثانية:(عندما x تسعى نحو عدد ما ولنفترض أنه a )

 

عندئذ فإن نهاية التابع الكسري عندما x تسعى نحو عدد

هي نهاية صورة العدد عندما x تسعى نحو ذلك العدد ونكتبها بالشكل:

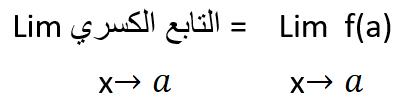
مثال: 

أوجد نهاية التابع (x)f :

 

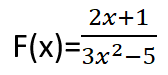
وذلك عندما

الحل:

  أولاً:  عندما X تسعى نحو الزائد لانهاية

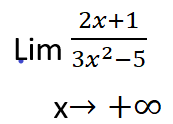
نلاحظ في هذا التابع أن الحد ان الحد المسيطر بالبسط هو 2x الذي يملك الأس الأعلى والحد المسيطر في المقام هو:

ومنه نكمل الحل بالشكل الآتي:

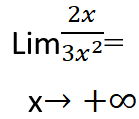
نختصر المجهول x في البسط مع المجهول x في المقام ،ثم نبدل المجهول x بالزائد لانهاية فيصبح التمرين بالشكل:

 

 

 

 

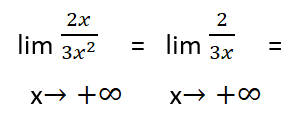
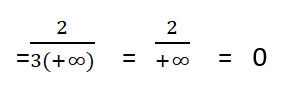
وهي الإجابة النهائية.

 

ثانياً:  عندما X تسعى نحو الناقص لانهاية

 

 

 

 

 

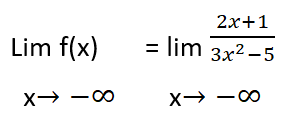
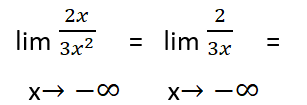
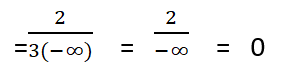
لمزيد من الأمثلة والشرح المفصل يمكنكم متابعة الفيديو الآتي: