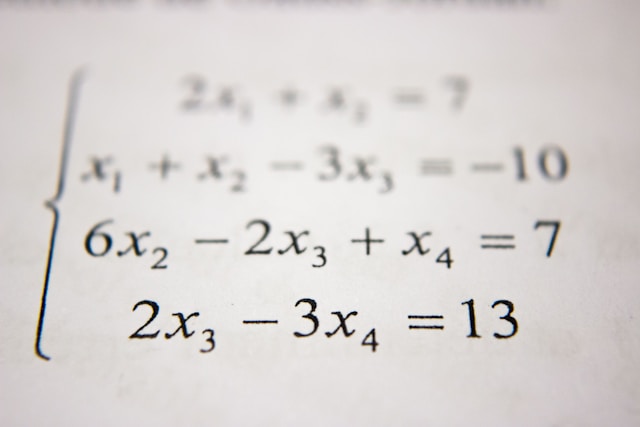سنتعلم في هذا الدرس من دروس الرياضيات كيفية تمثيل المعادلات بيانياً (أي رسم المستقيم الممثل للمعادلة الخطية) وذلك في المستوي الإحداثي المتمثل بالمقطعين السيني والصادي.
أولاً: ماهو المستوي الإحداثي:
هو عبارة عن المحورين المتعامدين م س ، م ص ، وكلا المحورين هما مستقيمي أعداد مرقمين بأعداد موجبة وأعداد سالبة.
المحور م س هو المحور الأفقي والمحور م ص هو المحور العمودي أو الشاقولي.
كما يتقاطع المحورين بالنقطة م ذات الإحداثيات (. ، . )
ثانياً:كيف نمثّل المعادلات الخطية بيانياً باستعمال المقطعين السيني والصادي:
سنشرح ذلك من خلال المثال الآتي:
مثال:
مثّل المعادلة الخطية
٢س + ٤ص = ١٦ بيانياً باستعمال المقطعين السيني والصادي.
الحل:
فكرة الحل: إنّ التمثيل البياني لهذه المعادلة هو عبارة عن مستقيم ولرسم أي مستقيم يجب علينا تعيين نقطتين على الأقل على المستوى الإحداثي المتمثل بالمقطعين السيني والصادي.
الحل:
تعيين النقطة الأولى:
لإيجاد المقطع السيني نضع ص=٠ ونعوّض بالمعادلة المعطاة فنجد:
٢س +٤ (٠ ) = ١٦
٢س = ١٦
هذه المعادلة وحيدة الخطوة لحلها نستخدم العملية المعاكسة للضرب وهي القسمة ، أي نقسّم كلا الطرفين على أمثال المتغير س (نقسم على العدد ٢) فيصبح حل المعادلة بالشكل:
س = ٨
أصبح لدينا النقطة الأولى ( ٨ ، ٠ )
تعيين النقطة الثانية:
لإيجاد المقطع الصادي نضع س=٠
ونعوّض في المعادلة المعطاة فنجد:
٢(٠) +٤ص=١٦
٤ص=١٦
نقسّم كلاّ الطرفين على أمثال المتغير س فنجد حل المعادلة:
ص=٤
ومنه فإنّ النقطة الثانية(٠، ٤)
نعيّن النقطتين اللتان أوجدانهما على المقطعين السيني والصادي ،ثمّ نصل بينهما فنحصل على المستقيم الممثل للمعادلة المعطاة ٢س+٤ص=١٦
وهو المطلوب.
ثالثا: فيديو عن الدرس
لمزيد من الشرح المفصّل شاهدوا الفيديو الآتي: