المتراجحات (المتباينة) من الدرجة الأولى، وكيفية حلّها – أ. فادية مغمومة

سنتعرف في هذا المقال على تعريف المتراجحات من الدرجة الأولى، وكيفية حلها وتمثيلها على مستقيم الأعداد .

شكل المتراجحات من الدرجة الأولى:

بدايةً المتراجحات تحتوي على أربع عناصر :
1. مجهول (متغير) من الدرجة الأولى
2.معاليم ( أعداد)
3.عمليات حسابية ( +،-،÷،×)
4. إحدى الإشارات أو ( أكثر ):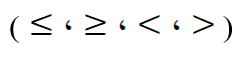> تعني أصغر تماماً

< تعني أكبر تماماً

 

 

 

أمثلة على بعض أشكال المتراجحات:

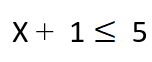
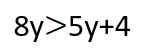
حل المتراجحات من الدرجة الأولى:

تحل المتراجحات من الدرجة الأولى كما تحل المعادلات من الدرجة الأولى ، وذلك:

1.بنقل المعاليم إلى طرف والمجاهيل إلى الطرف الآخر مع تغيير إشارة الحد المنقول

2.ثم بجمع الأمثال المتشابهة ( إن وجدت)

3.ثمّ بالتقسيم على أمثال المجهول إن كان له أمثال غير العدد واحد

وسنحل الأمثلة التي ذكرناها في الفقرة السابقة لتوضيح هذه الخطوات .

أمثلة:

حل كلاً من المتراجحات الآتية:

مثال1:

 

 

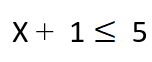
لحل هذه المتراجحة نطبق الخطوات التي ذكرناها آنفاً.

الخطوة الأولى ننقل المجاهيل إلى طرف والمعاليم إلى طرف مع تغيير إشارة الحد المنقول ، ثم جمع الأمثال المتشابهة فيصبح الحل بالشكل:

 

 

 

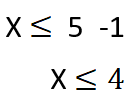
وهو حل المتراجحة النهائي.

 

مثال2:

 

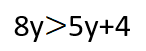
الحل:

نتبع الخطوات السابقة:

ننقل المعليم إلى طرف والمجاهيل إلى طرف مع تغيير إشارة الحد المنقول ثم نجمع الحدود المتشابهة فتصبح المتراجحة بالشكل:

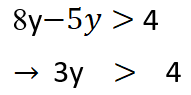
ثم نقسم على أمثال المجهول وهو العدد 3 فنص إلى الحل المطلوب:

 

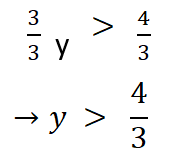
مثال3:

الحل:

باتباع الخطوات التي ذكرناها بالأمثلة السابقة نجد الحل بالشكل:

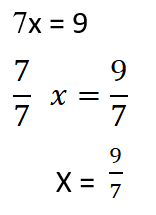
تمثيل المتراجحات على مستقيم الأعداد:

لتمثيل المتراجحات على مستقيم الأعداد يجب علينا اتباع الخطوات الآتية:

1. نقوم بحل المتراجحة

2. ثمّ نرسيم مستقيم أعداد ونقوم بتقسيمه إلى سنتيمترات

3. ثمّ نضع عليها الأعداد الموجبة والأعداد السالبة

4. ثم نقوم بتمثيل الحل كما وتحديد الحلول المقبولة والحلول المرفوضة على مستقيم الأعداد

لفهم كيفية تمثيل حل المتراجحات على مستقيم الأعداد ولمزيد من الأمثلة والشرح المفصّل شاهدوا الفيديو: