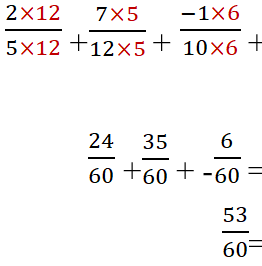دروس الرياضيات: جمع وطرح الكسور

سنتعلم في هذا الدرس كيفية جمع وطرح الكسور مع إعطاء أمثلة توضيحية على ذلك.

ماهو الكسر:

يتألف الكسر من عددين (قد يكونا طبيعيين أو صحيحين أو حتى حقيقيين)

العدد الأول موجود بالبسط والعدد الثاني موجود بالمقام، ويوجد بين البسط والمقام حد الكسر أو (خط الكسر)

مثال:

حيث أن العدد 3 هو بسط الكسر

والعدد 4 هو مقام الكسر

والخط الذي بينهما هو حد الكسر

كيف نجمع ونطرح الكسور:

لدينا حالتين:

الحالة الأولى: عندما تكون المقامات موحدة (أي تملك نفس المقامات)

في هذه الحالة نبقي المقامالكسور نفسه ونجري عملية جمع أو طرح البسوط ، ثمّ نجري عملية اختزال الناتج إن كان يقبل الاختزال

مثال:

أوجد ناتج مايلي واكتبه بأبسط صورة

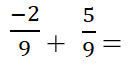
في هذا المثال الكسرين يملكان المقام نفسه وهو العدد 9 ، لذا نطبق القاعدة السابقة ألا وهي: نبقي المقام نفسه ونجري عملية جمع أو طرح البسوط ، ثمّ نجري عملية اختزال الناتج إن كان يقبل الاختزال

فينتج:

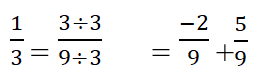
الحالة الثانية: عندما تكون المقامات غير موحدة (مختلفة)

في هذه الحالة يجب علينا توحيد المقامات وذلك بإيجاد عددين مختلفين نضربهما بالمقامين كي يصبحا موحديين ، ولكن يجب علينا ضرب هذان العددان بالبسوط أيضاً كي لاتتغير قيمة الكسر

أو هناك طريقة أخرى غير الطريقة السابقة التي هي عبارة عن تخمين ماهما العددان الذان يجب أن نضرب بهما

وهي: إيجاد المضاعف المشترك الأكبر للمقامات ثمّ تقسيم هذا المضاعف على المقامات لنحصل على العدد الذي يجب أن نضرب به وسنعطي أمثلة توضح ذلك:

مثال1:

أوجد ناتج مايلي واكتبه بأبسط صورة.

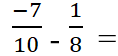
الحل:

نلاحظ هنا اختلاف المقامات لذا يجب علينا أن نقوم بتوحيدها وذلك بإحدى الطريقتين السابقتين، لنتبع الطريقة الأولى ونخمن عددين أحدهما نضربه بالعدد 10 والآخر نضربه بالعدد 8 حتى نحصل على مقامات موحدة ، وللسهولة نضرب العدد 10 بالعدد 8 ونضرب العدد 8 بالعدد 10 فنحصل على المقام المشترك 80 ، ولكن كما ذكرنا سابقاً لاننسى أن نضرب البسوط أيضاً كي لاتتغير قيمة الكسور، ثمّ نقوم بعملية اختزال الناتج لأبسط صورة

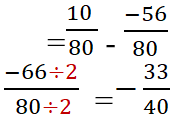
مثال2:

أوجد ناتج مايلي واكتبه بأبسط صورة

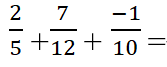
الحل:

نلاحظ هنا أنه يصعب علينا تخمين ماهي الأعداد التي يجب أن نضربها بالمقامات حتى تتوحد، لذا سنلجئ إلى الطريقة الثانية وهي إيجاد المضاعف المشترك الأصغر للمقامات ثمّ تقسيم هذا المضاعف على المقامات لنحصل على الأعداد المطلوبة لتوحيد المقامات

مضاعفات العدد5 :

…..5،10،15،20،25،30،35،40،45،50،55،60،65

مضاعفات العدد 10:

……10،20،30،40،50،60،70،80

مضاعفات العدد 12:

……12،24،36،48،60،72

نلاحظ أن أصغر عدد موجود في مضاعفات الأعداد الثلاثة هو العدد 60 لذا فإنّ المضاعف المشترك الأصغر للأعداد الثلاثة هو العدد 60

نقسم العدد 60 على الأعداد:

5/60=12

10/60=6

12/60=5

ومنه نستطيع الآن بكل سهولة ضرب المقام 5 بالعدد 12 ، وضرب المقام 10 بالعدد 6 وضرب المقام 12 بالعدد 5 وذلك حتى نحصل على مقامات موحدة، ولكن لاننسى ضرب البسوط أيضاً بهذه الأرقام وذلك بالشكل الآتي: