الزاويتان المتقابلتان بالرأس،الزاويتان المتكاملتان،الزاويتان المتتامتان

سنتعلم في هذا الدرس من دروس الرياضيات تعريف الزاويتين المتقابلتين بالرأس وكيف نستفيد من قياس الزاويتين المتقابلتين بالرأس في حل المسائل الرياضية.

أولاً- مما تكون الزاوية:

إنّ كل زاوية في المستوى تتكون من رأس وضلعين كما في المثال الآتي:

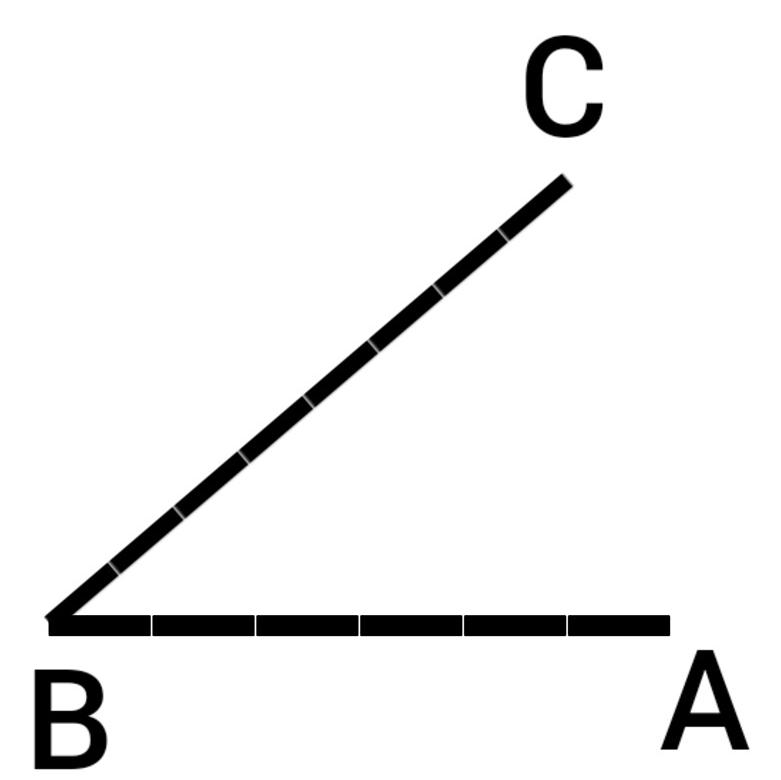
الزاوية ABC رأسها B وضلعاها AB ,AC .

ثانياً- الزاويتان المتقابلتان بالرأس:

هما زاويتان لهما رأس مشترك و أضلاعهما امتداد لبعضها (أي تقع على نفس الاستقامة).
مثال:

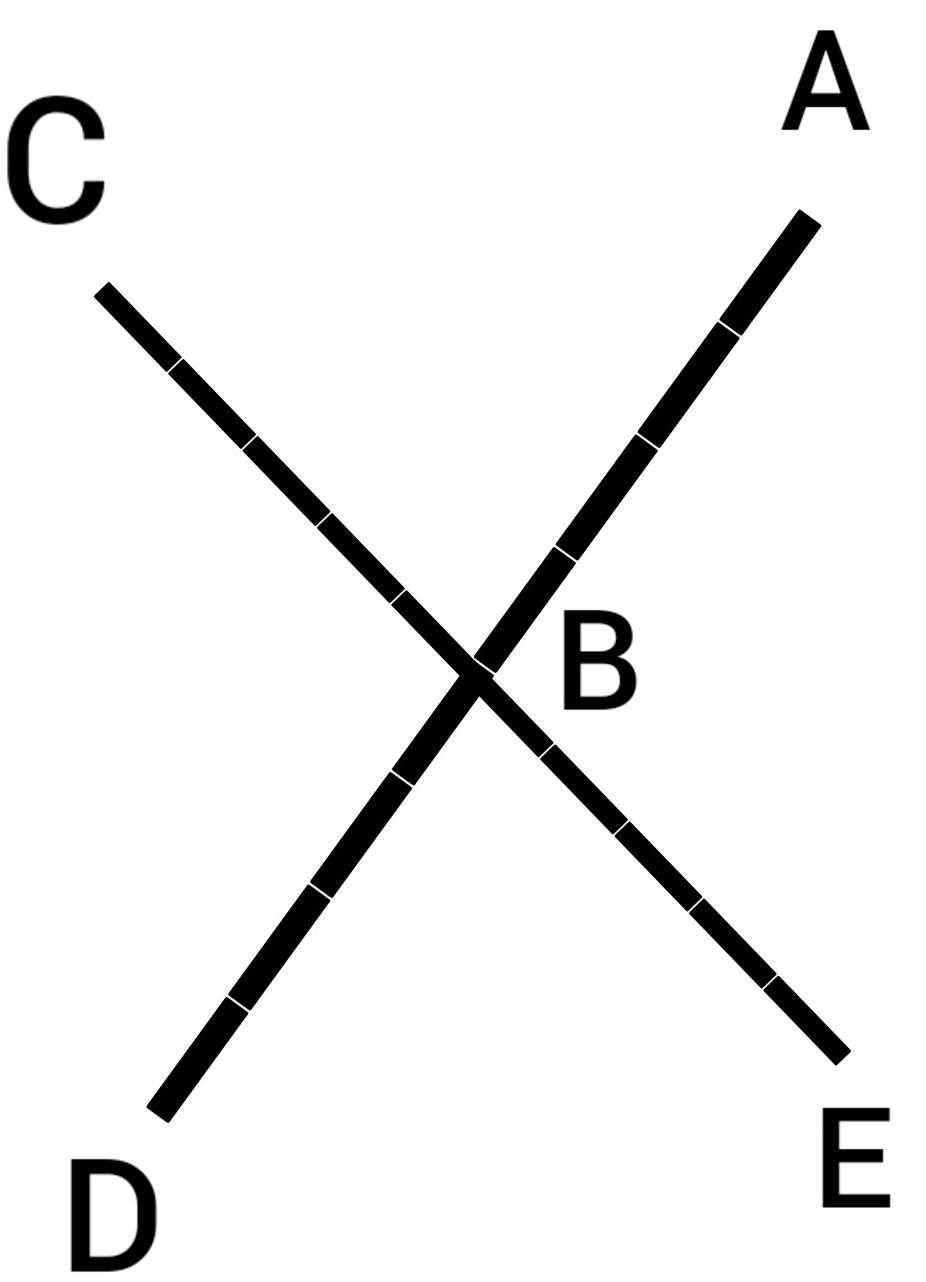
الزاويتان ABC,DBE هما زاويتان متقابلتان بالرأس رأسهما المشترك هو B و الضلع AB في الزاوية ABC امتداد للضلع BD في الزاوية DBE و الضلع BC في الزاوية ABC امتداد للضلع BE في الزاوية DBE .

ثالثاً- الزاويتان المتقابلتان بالرأس متطابقتان (أي أن لهما نفس القياس)

في المثال السابق لو كان قياس الزاوية ABC =60 أوجد قياس
DBE
الحل:
إنّ الزاويتبن ABC و DBE زاويتان متقابلتان بالرأس .
والزاويتان المتقابلتان بالرأس متطابقتان لذا فإنّ قياس DBE =60

رابعاً- الزاويتان المتكاملتان:

هما زاويتان مجموع قياسهما 180 درجة ،قد تكونا متجاورتان كما في الشكل:

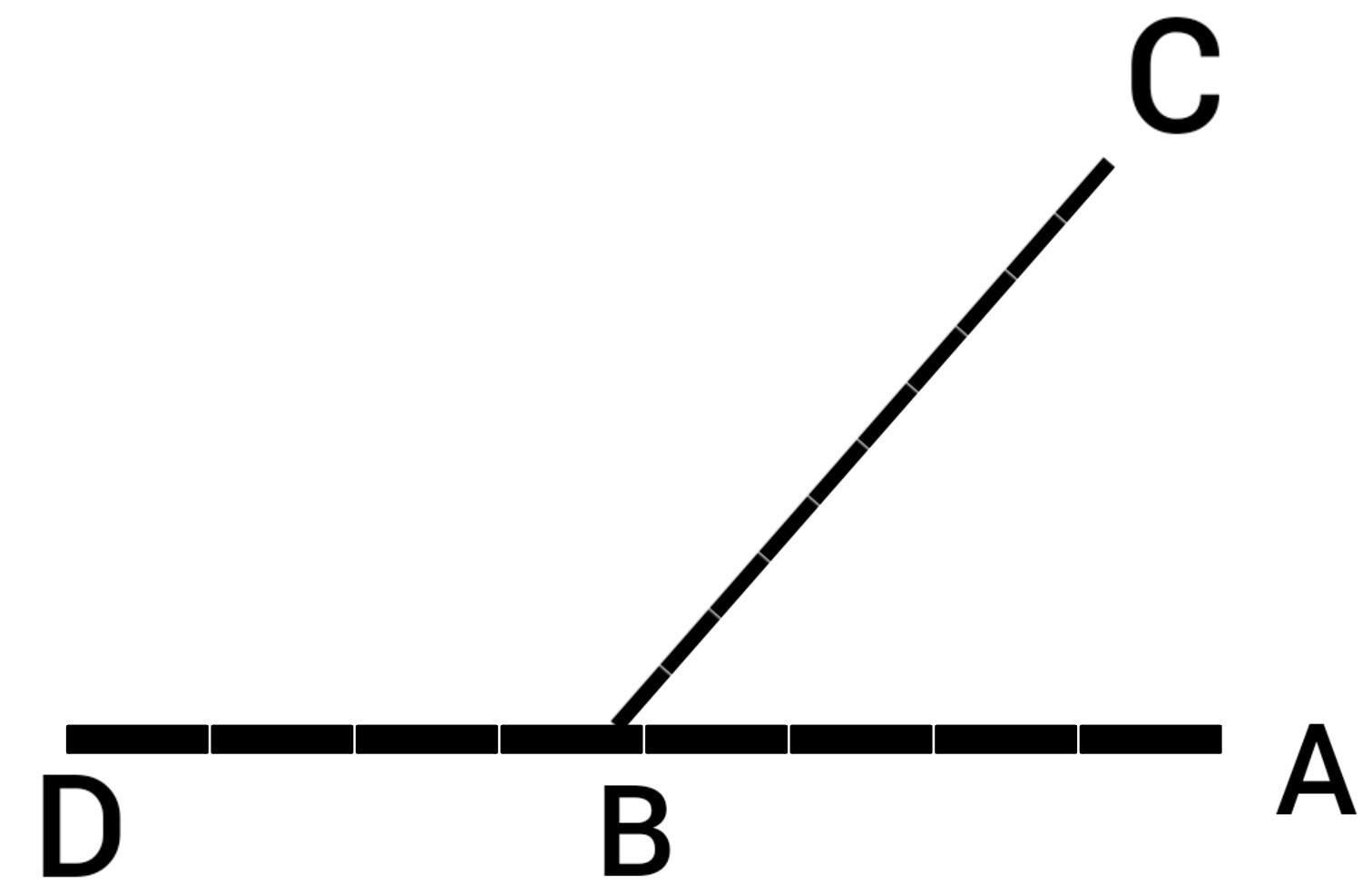
حيث إنّ الزاويتان المتجاورتان هما ABC ،CBD
وعندئذ يكون لهما رأس مشترك وهو في الشكل السابق B
ويكون لهما ضلعان على نفس الاستقامة أي تشكلان مستقيم وهو المستقيم AD
وقد تكونا غير متجاورتان كما في الشكل :

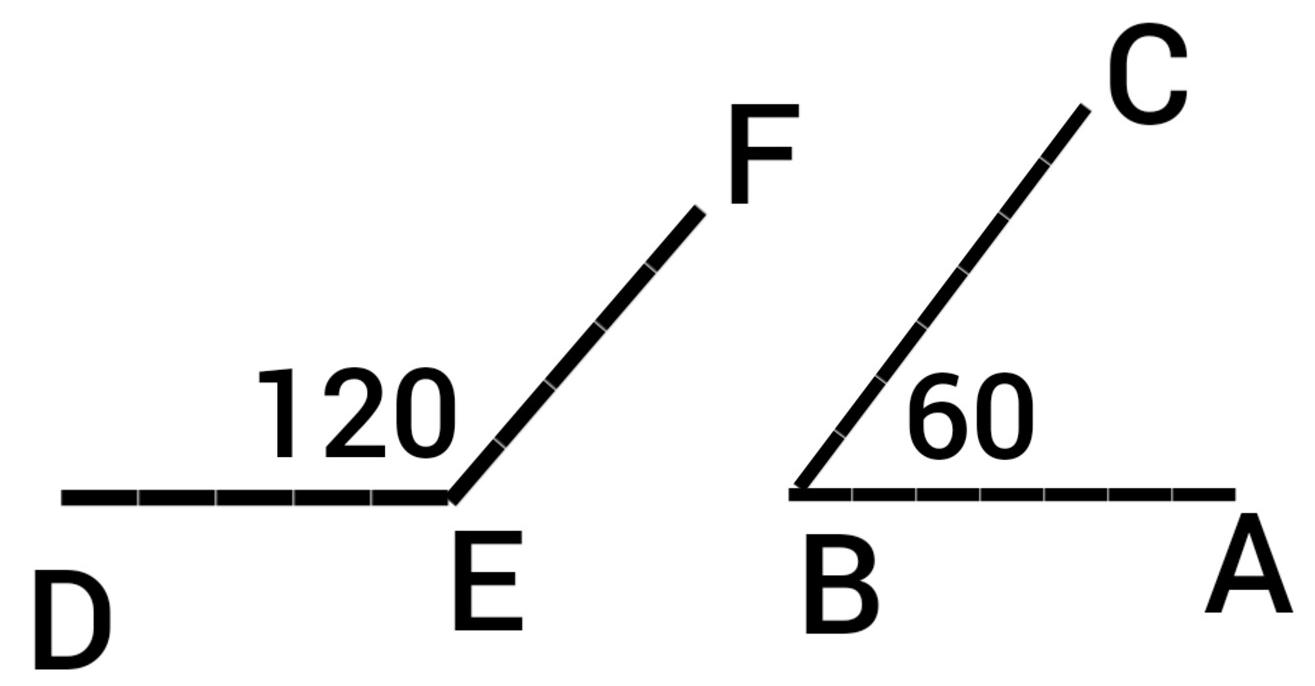
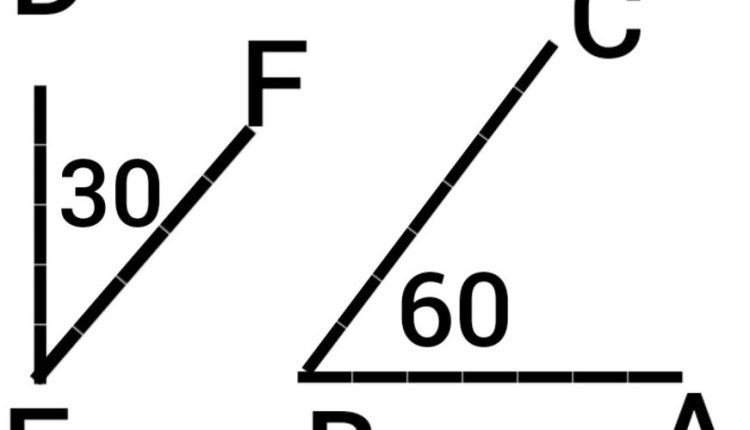
حيث أنّ الزاويتان ABC , DEF هما زاويتان متكاملتان لأنّ مجموعهما 180 درجة

خامساً- الزاويتان المتتامتان:

هما زاويتان مجموعهما 90 درجة
كذلك الأمر قد تكون الزاويتان المتتامتان متجاورتان كما في الشكل:

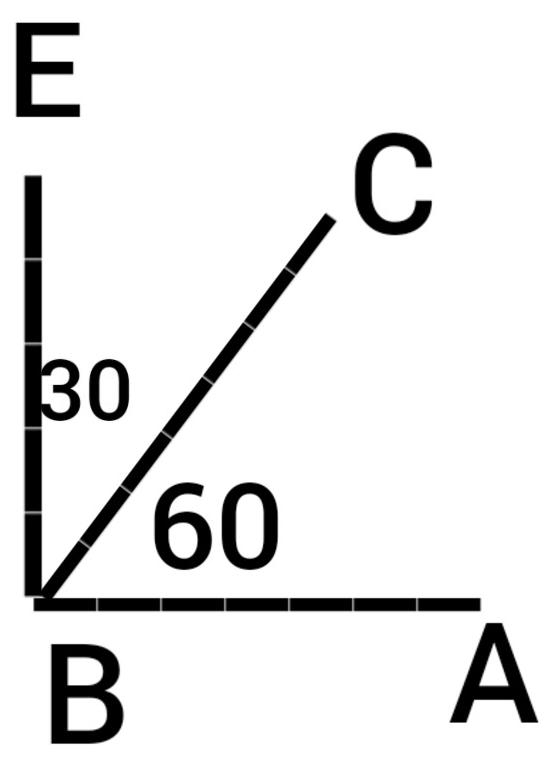
حيث إنّ الزاويتين ABC,CBE متتامتان؛ لأنّ مجموعهما 90 درجة
وقد تكونا غير متجاورتين كما في الشكل الآتي:

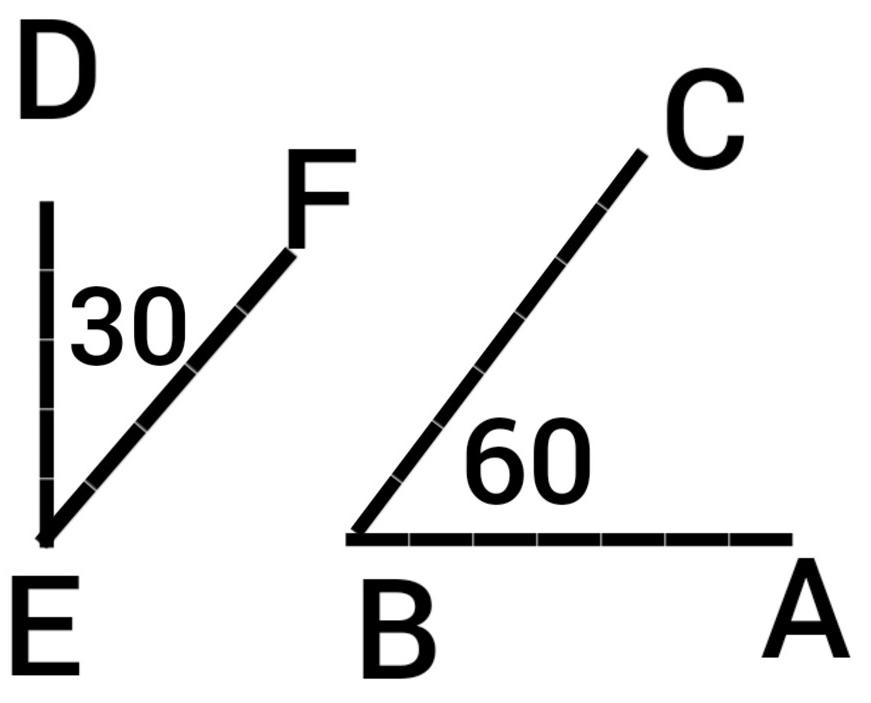
حيث إنّ الزاويتين ABC ، DEF متتامتان لأن مجموع قياسهما يساوي 90 درجة ولكنهما غير متجاورتين.

سادسًا- فيديو تعليمي:

ولمزيد من الفائدة ندعوكم إلى مشاهدة هذا الفيديو: