دروس الرياضيات: حجم الهرم وحجم الكرة للصف التاسع

سنتعلم في هذا الدرس من دروس الرياضيات قوانين إيجاد حجم الهرم وحجم الكرة وسنعطي أمثلة عديدة لتطبيق هذه القوانين

قانون حجم الكرة:

 

 

 

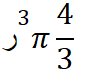
حيث أن العدد

هو عدد ثابت ويساوي تقريباً 3.14 أو 22/7 ولانعوّض بقيمته إذا لم يعطونا قيمته في نص المسألة

والعدد ر هو نصف قطر الكرة

 

مثال:

أوجد حجم الكرة الآتية:

 

 

 

 

 

 

 

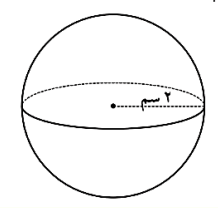
الحل:

نلاحظ أن نصف قطر الكرة هو 2 سم

نكتب قانون حجم الكرة أولاً ثمّ نعوض ر (نصف القطر )بقيمته فنجد

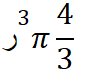
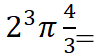
إنّ العدد 2 أس 3 يعني 2*2*2 ويساوي 8 نعوّض به ثمّ نضربه بالكسر 4/3 وذلك بضرب البسط بالبسط ( اي نضرب العدد 8 بالعدد 4 ) والمقام بالمقام ( أي نضرب العدد 3 بالعدد 1 لأن الكسر الذي لايملك مقام يكون مقامه 1 )

فيصبح الناتج النهائي بالشكل:

 

 

 

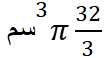
مثال2:

كرة نصف قطرها 5 سم احسب حجمها.

الحل:

نكتب قانون حجم الكرة ثمّ نعوّض بالأرقام فنجد

 

 

 

 

 

 

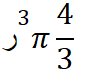
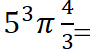
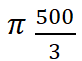
سم للتكعيب

حجم الهرم:

إنّ حجم الهرم يعطى بالعلاقة:

1/3 مساحة القاعدة * الارتفاع المتعلق بها

ونرمز لذلك بالرموز بالشكل:

 

 

 

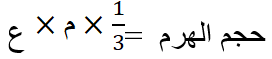
حيث يقصد بالحرف م: مساحة القاعدة ( قد تكون القاعدة مثلثاً أو مربعاً أو مضلع خماسي أو سداسي ……الخ)

ويقصد بالحرف ع: الارتفاع

 

مثال1:

هرم رباعي قاعدته مربع طول ضلعه 2 سم ، وارتفاعه 3 سم ، أوجد حجمه.

 

 

 

 

 

 

 

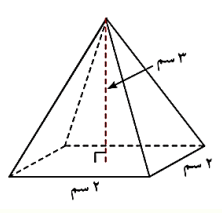
الحل:

نكتب أولاً قانون حجم الهرم الذي ذكرناه آنفاً

 

 

 

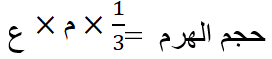
يجب علينا إيجاد مساحة القاعدة ، وبما أنّ القاعدة هي عبارة عن مربع فعلينا تطبيق قانون مساحة المربع

مساحة المربع = طول الضلع * طول الضلع

م = 2*2= 4

الآن نستطيع تطبيق قانون حجم الهرم

حجم الهرم = 1/3 * 4 * 3 = 4

 

مثال2:

هرم قائم مساحة قاعدته 6 سم مربع ، وارتفاعه 10 سم ، احسب حجمه

الحل:

نكتب قانون حجم الهرم ثمّ نعوّض بالأرقام فنجد:

 

 

 

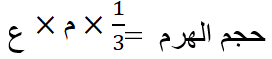
حجم الهرم = 1/3 * 6 * 10 = 2 *10 = 20 سم مكعب