سنتعلم في هذا الدرس من دروس الرياضيات كيف نحلل ثلاثية الحدود من النمط:

لتحليل ثلاثية الحدود السابقة لدينا ثلاث حالات :
الحالة الأولى: عندما يكون ب ، ج موجبين
نوجد عددين صحيحين م ، ن موجبين بحيث يكون مجموعهما يساوي ب وناتج ضربهما يساوي ج ثم نكتب :

على الشكل:
( س + م ) ( س + ن ) ، حيث م + ن = ب و م ن = ج
مثال: حلل ثلاثية الحدود
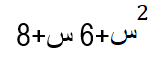
الحل:
طريقة الحل: نبحث عن عددين موجبين بحيث يكون ناتج جمعهما يساوي 6 وناتج ضربهما يساوي 8
ولإيجاد هذين العددين بسهولة نكتب كل الأعداد الموجبة التي يكون حاصل ضربها يساوي 8 ثمّ نختار منها العددان اللذان يكون حاصل جمعهما يساوي 6
الأعداد التي جداؤها يساوي العدد 8 هي:
1 * 8 = 8
2 * 4 = 8
ثمّ نختار عددان من بين هذه الأعداد مجموعهما يساوي العدد 6 فنلاحظ بسهولة أن العددان اللذان يكون ناتج جمعهما يساوي العدد 6 هما العددان:
2 ، 4 فتكتب نتيجة التحليل بالشكل:
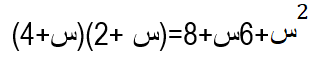
مثال2:
حلل ثلاثية الحدود الآتية:
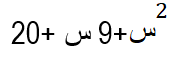
طريقة الحل: نحلل بنفس طريقة المثال السابق وذلك بالبحث عن عددين صحيحين موجبين بحيث يكون ناتج ضربهما يساوي العدد 20 وناتج جمعهما يساوي العدد 9
نبحث أولاً عن عددين ناتج ضربهما يساوي العدد 20
الأعداد هي:
20 * 1 = 20
5 * 4 = 20
10 * 2 = 20
ونبحث من بين هذه الأعداد عن العددين اللذين يكون ناتج جمعهما يساوي العدد 9 فنلاحظ أن الععدان هما 4 ، 5
فنكتب ناتج تحليل العبارة بالشكل:
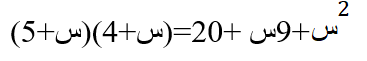

الحل:
أ) لتحليل كثيرة الحدود نحل بنفس طريقة المثالين السابقين ، وذلك بأن نبحث عن عددين جداؤهما يساوي العدد 24 وناتج جمعهما يساوي العدد 11
نكتب جميع الأعداد التي يكون جداؤها يساوي العدد 24 وهي:
24 *1 = 24
12 * 2 = 24
6 * 4 =24
8 * 3 =24
ونبحث بين هذه الأعداد عن العددين اللذين يكون ناتج جمعهما يساوي 11 فنلاحظ بسهولة أن العددين هما 8 ، 3
فتكون نتيجة التحليل هي :
( د + 3 ) ( د + 8 )
الحالة الثانية: عندما تكون ب سالبة و ج موجبة
مثال:
حلل ثلاثية الحدود الآتية:
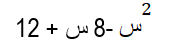
بما أن ج موجبة و ب سالبة في ثلاثية الحدود أي ب = -8 و ج = +12 لذا يجب علينا إيجاد عددين سالبين بحيث يكون مجموعهما – 8 وناتج ضربهما يساوي العدد 12
ولنكتب أولاً جميع الأعداد ( بحيث يكون العددين سالبين ) التي يكون ناتج جداؤها يساوي العدد 12 وهي:
-12 * -1 = 12
-4 * – 3 = 12
– 6 * – 2 = 12
نختار من هذه الأعداد العددين اللذين يكون مجموعهما يساوي العدد – 8 فنلاحظ بسهولة أن العددين هما -6 ، -2
ونكتب ناتج تحليل ثلاثية الحدود بالشكل:
= ( س – 6 ) ( س – 2 )

الحل:
أ) في هذا التمرين يجب علينا إيجاد عددين بحيث يكون ناتج جداؤهما يساوي العدد 21 وناتج مجموعهما يساوي – 22
نكتب أولاً جميع الأعداد الصحيحة ( نختار العددين سالبين ) التي يكون جداؤها يساوي العدد 21 وهي:
-21 * -1 = 21
-7 * – 1=21
نختار من بين هذه الأعداد العددين اللذين يكون ناتج جمعهما يساوي -22 فنلاحظ بسهولة أن العددين هما: -21 ، -1
فيكون ناتج التحليل بالشكل:
( م – 1 )( م -21 )
ب) بنفس الطريقة في التمارين السابقة علينا إيجاد عددين سالبين جداؤهما +28 وناتج مجموعهما يساوي العدد -11
نكتب أولاً جميع الأعداد الصحيحة التي يكون جداؤها يساوي العدد 28 وهي:
-28 * -1 = 28
-14 * -2 = 28
-7 * -4 = 28
ونختار من بين هذه الأعداد العددين اللذين يكون مجموعهما يساوي -11 فنلاحظ بسهولة أن العددين هما – 7 و -4
نكتب ناتج التحليل بالشكل:
= ( و – 7 ) ( و – 4 )
الحالة الثالثة: عندما تكون ج سالبة
مثال1 : حلل ثلاثية الحدود
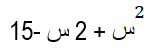
في ثلاثية الحدود هذه لدينا ب = + 2 و ج = -15 وبما أن ج سالبة فإن: م و ن عددان مختلفان بالإشارة
وبما أن ب موجبة فالعدد الذي تكون قيمته المطلقة أكبر هو العدد الموجب
الحل: نختار عددين بحيث يكون جداؤهما يساوي -15 ( على أن يكون أحدهما موجباً والآخر سالباً )
الأعداد هي:
15 * -1 = -15 ( القيمة المطلقة للعدد 15 أكبر من القيمة المطلقة للعدد 1 لذا فإن القيمة الموجبة هي للعدد 15 والقيمة السالبة هي للعدد 1 )
-3 * +5 = – 15
نلاحظ أن ناتج جمع العددين + 5 ، -3 هي +2 لذا فسنختار هذين العدديين فتصبح نتيجة التحليل بالشكل:
( س -3 ) ( س + 5 )
مثال 2: حلل ثلاثية الحدود الآتية
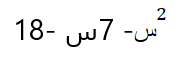
الحل: نلاحظ في هذا التمرين أن ب = -7 و ج= -18 إذاً م أو ن سالبة وليس كلاهما وبما أن ب سالبة فيكون العدد الذي قيمته المطلقة أكبر هو العدد السالب ، ثمّ نحلل بنفس طريقة التمرين السابق وذلك بإيجاد عددين ناتج ضربهما يساوي -18 ( بحيث يكون أحدهما موجب والآخر سالب ) ويكون ناتج جمعهما يساوي -7
أولاً نبحث عن عددين ناتج جداؤهما يساوي العدد -18 ونكتبها:
-18 * +1 = -18 ( اخترنا الاشارة السالبة للعدد 18 لأن قيمته المطلقة أكبر )
+2 * -9 = -18 ( اخترنا الاشارة السالبة للعدد 9 لأن قيمته المطلقة أكبر )
-6 * +3 = -18 ( اخترنا الاشارة السالبة للعدد 6 لأن قيمته المطلقة أكبر )
ثمّ نختار العددين اللذين يكون ناتج جمعهما يساوي العدد -7 فنلاحظ بسهولة أن العددين هما +2 ، -9 فتصبح نتيجة التحليل بالشكل:
( س + 2 ) ( س – 9 )