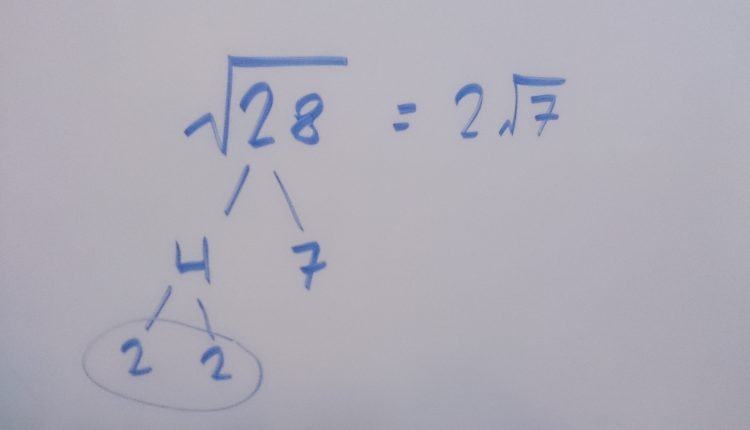أنواع الجذور: تبسيط الجذور التربيعية

في درسنا أنواع الجذور سنتحدث عن تبسيط الجذور التربيعية التي يقصد بها إيجاد أبسط صورة للعدد الواقع تحت الجذر ، بحيث نستطيع التخلص من الجذر بشكل نهائي أو جعل العدد الواقع تحت الجذر عدد أولي ، أو عدد لايمكن تبسيطه .

أمثلة:

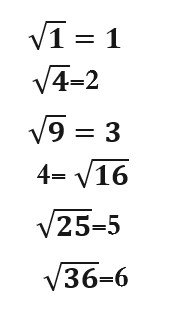                    وناتج هذه الجذور ينتج عن إيجاد عدد نضربه بنفسه لنصل على العدد الموجود تحت الجذر

ولكن هناك أعداد ليس لها جذر مباشر كجذر العدد 8 مثلا لايوجد عدد نضربه بنفسه لينتج 8  فهنا يلزمنا إيجاد طريقة لتبسيطه

الطريقة:

نبحث عن عددين ضربهما 8  أحدهما أولي والثاني له جذر ، فنجد العددين 4 ,2  حيث أن العدد 4  عدد له جذر وجذره 2  والعدد 2  هو عدد أولي ،نجذر العدد 4  وجذره 2 نخرجه خارج الجذر ونبقي العدد الأولي وهو العدد 2  تحت الجذر .

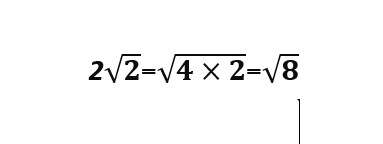
وبنفس الطريقة نوجد جذر العدد 32

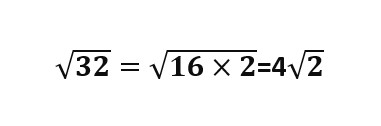
حيث إن العدد 32  ناتج عن ضرب العدد 16  الذي جذره العدد 4  والعدد الأولي 2

فنجذر العدد 16  ونخرج ناتج الجذر خارج الجذر ونبقي العدد الأولي 2  تحت الجذر

لنعطي مثالاً أخيرًا :

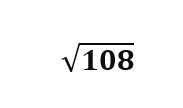
بنفس الطريقة نبحث عن عددين جداؤهما 108 أحدهما أولي والآخر له جذر

ولسهولة ايجاد هذين العددين نقسم العدد 108 على الأعداد الأولية ونبدأ بأصغرها وهو العدد 2 ، عند تقسيم العدد 108 على العدد 2  يكون الناتج 54 ونلاحظ أن هذا العدد ليس له جذر مباشر ، لذلك نتابع قسمة العدد 108 على الأعداد الأولية الأخرى ، نقسمه على العدد 3 نحصل على الناتج 36 ،نلاحظ أن للعدد 36جذر وهو العدد 6، فنستنتج أن هذا هو الاختيار الصحيح حتى نتابع في الحل:

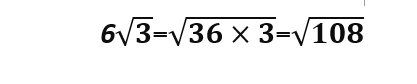
 تجدون في الفيديو التالي الشرح الكامل لهذا الموضوع