دروس الرياضيات: حساب طول ضلع في مثلث قائم

سنتعلم في هذا الدرس من دروس الرياضيات كيفية حساب طول ضلع في مثلث قائم بمعرفة إحدى النسب المثلثية:(جيب،تجيب،ظل) أو مايعرف في أغلب المناهج ب:( Sin،cos،tan)

في البداية لدينا المثلث القائم ABC:

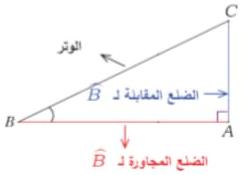
سنكتب قوانين النسب المثلثية للزاوية الحادة B بعد معرفة الضلع المقابلة لها والضلع المجاورة والوتر كما هو موضح بالشكل المرسوم السابق

قوانين النسب المثلثية:

انطلاقاً من هذه القوانين فإننا مثلاً بمعرفة sin زاوية نستطيع إيجاد طول الضلع المقابلة لهذه الزاوية أو نستطيع إيجاد طول الوتر.

وبمعرفة cos زاوية نستطيع إيجاد طول الضلع الم[h,vm لهذه الزاوية أو  طول الوتر.

وبمعرفة tan زاوية نستطيع إيجاد طول الضلع المقابلة لهذه الزاوية أو نستطيع إيجاد طول الضلع المجاورة لها.

وذلك من خلال الخطوات:

1.بكتابة القانون

2.تعويض الرموز

3.تعويض المعطيات

4.إجراء التناسب

مثال1:

ABC مثلث قائم في B فيه:

BC=8

SinBAC=4/5 ، احسب طول الوتر.

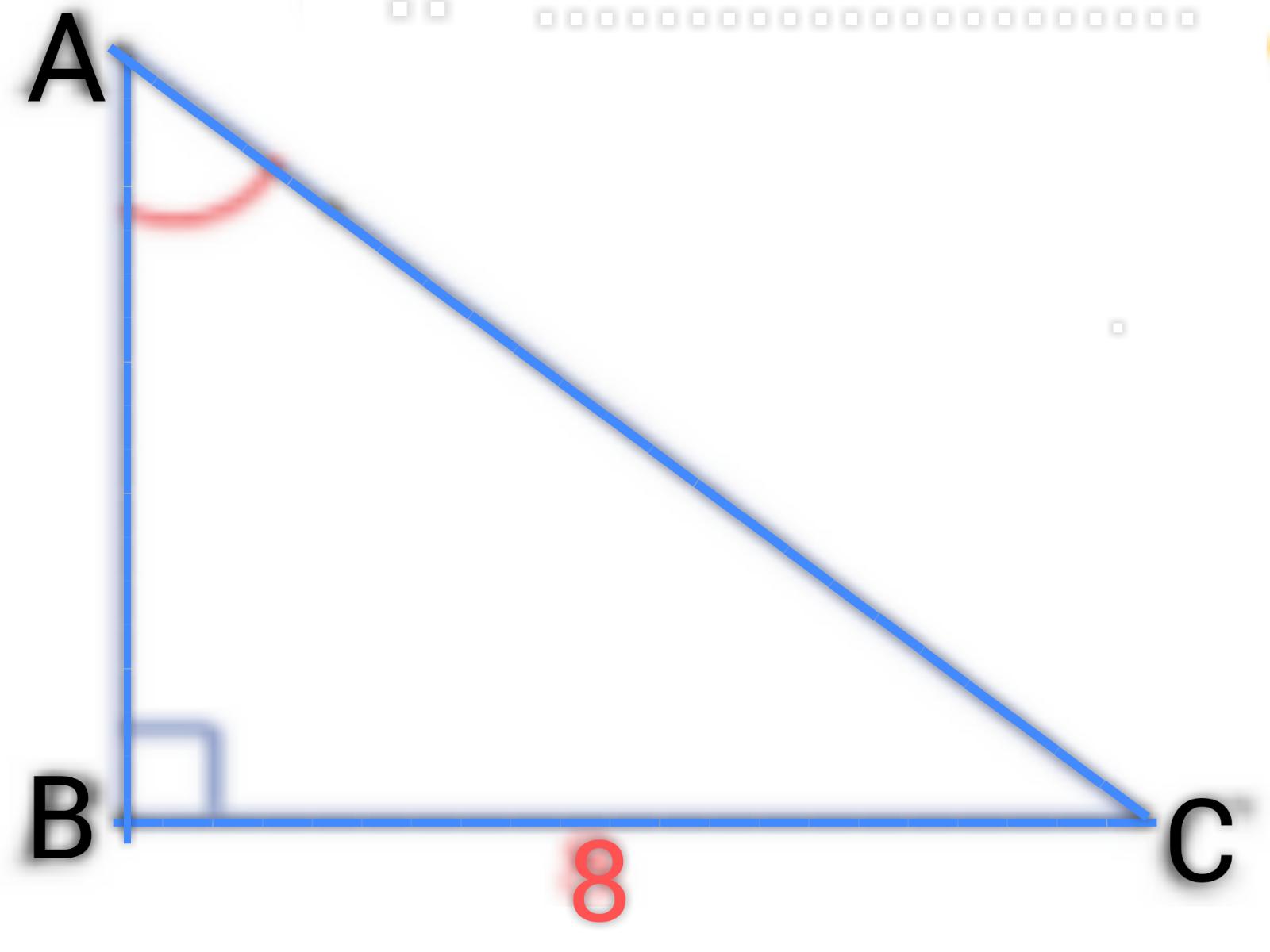
الحل:

في هذا المثال لدينا SIN الزاوية B هو المعلوم لهذا يجب علينا تطبيق قانون ال SIN ثمّ اتباع الخطوات التي ذكرناها آنفاً لإيجاد الضلع المطلوب ألا وهو الوتر AC .

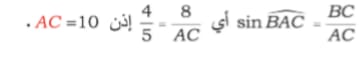مثال2:

المثلث EFG مثلث قائم في E، فيه:

FG=7.5

Cos EFG=2/3 والمطلوب:

احسب الطول FE.

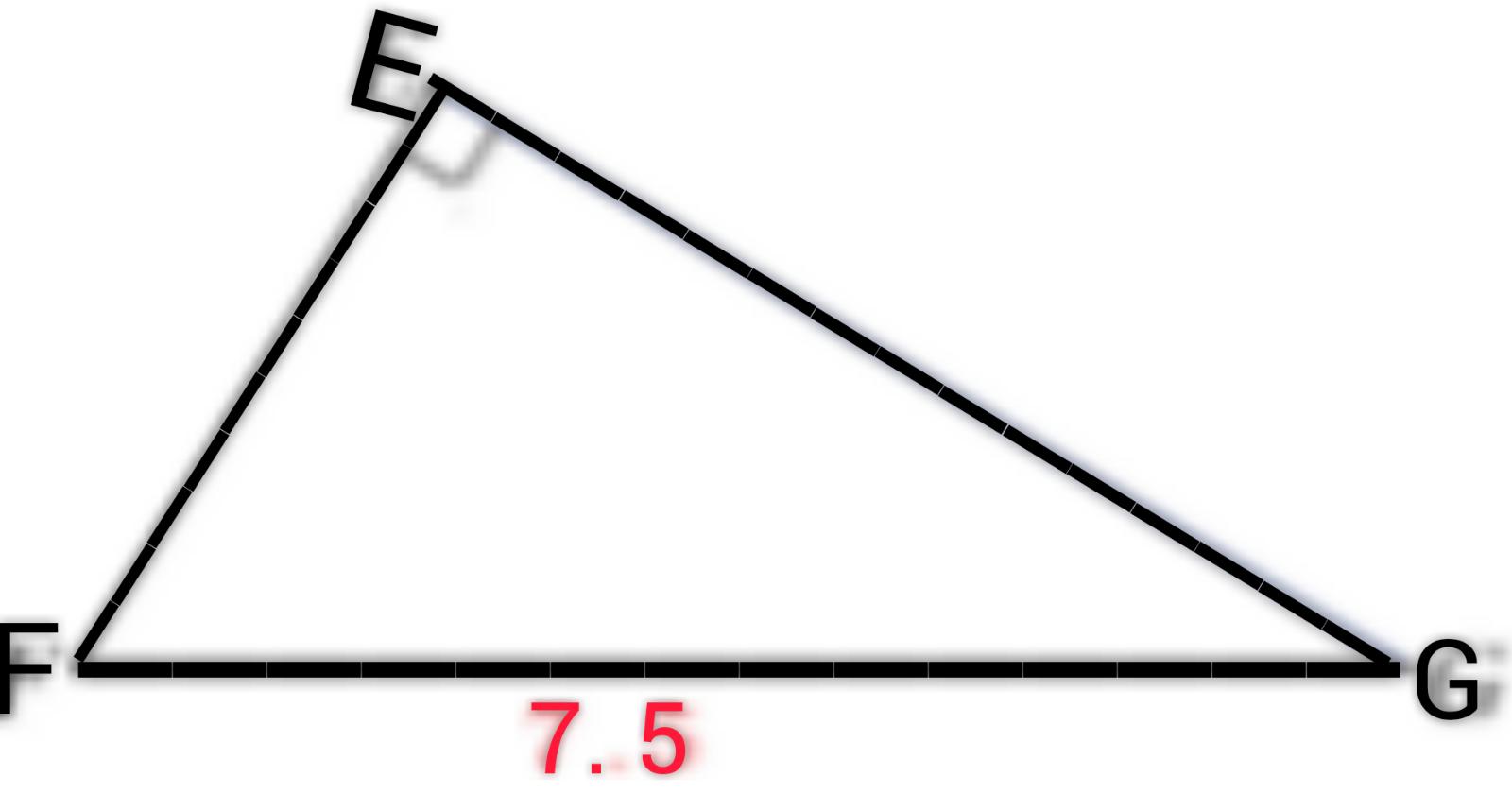
الحل:

نطبق قانون  COS الزاوية EFG لنحصل على طول الضلع FE المطلوب وذلك باتباع الخطوات الآتية:

مثال3:

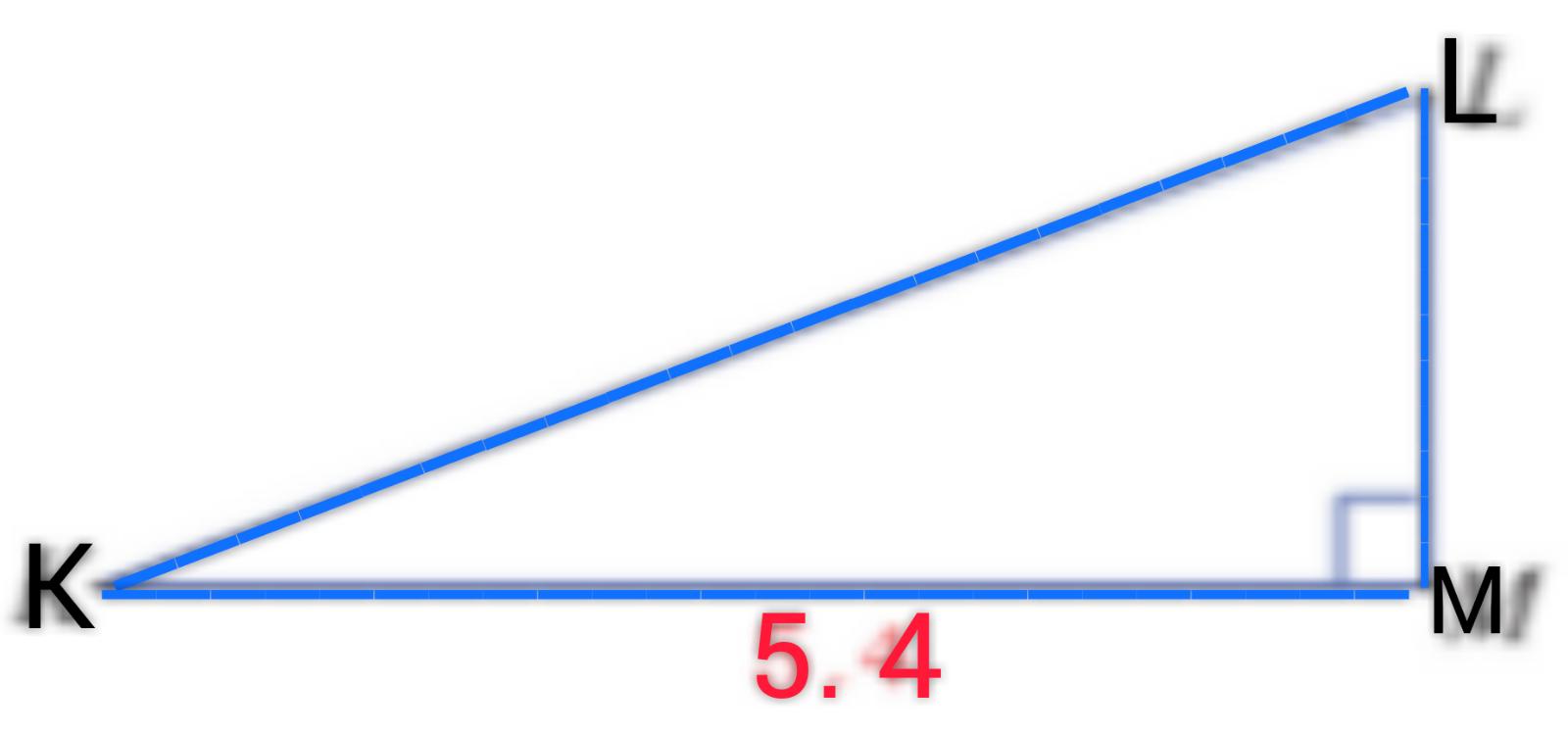
المثلث KLM مثلث قائم في M، فيه:

KM=5

TanMKL=1/3 والمطلوب:

احسب الطول ML.

الحل:

نطبق قانون TanMKL وذلك لحساب الطول ML وذلك باتباع الخطوات الآتية:

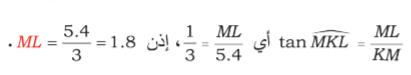
ولمزيد من الفائدة ندعوكم لمشاهدة هذين الفيديوين حيث ستجدون الدرس مشروحا بالصوت والصورة:

(1)

(2)