دروس الرياضيات: نظرية فيثاغورث مع شرح أمثلة عليها
سنتعرف في هذا المقال على نظرية فيثاغورث من اكتشفها،ماهو نصها، متى نستخدمها، وسنعطي أمثلة على كيفية تطبيقها.
أولاً: من اكتشفها
سميث نظرية فيثاغورث بهذا الاسم نسبةً إلى العالم فيثاغورس الساموسي (570 – 495 ق.م) هو فيلسوف وعالم رياضيات يوناني ، مؤسس الحركة الفيثاغورثية (فيثاغورث) المشهورة.
ثانياً: متى نستخدمها
تستخدم نظرية فيثاغورث في المثلث القائم عندما يكون لدينا ضلعين معلومين فيه وضلع مجهول يُطلب إيجاد طوله.
ثالثاً: ماهو نص نظرية فيثاغورث:
النص: مربع الوتر يساوي مجموع مربعي الضلعين القائمين
رابعاً: كيفية استخدامها
عندما يكون لدينا مثلث قائم الزاوية (فيه زاوية قائمة قياسها يساوي 90 درجة) ، وداخل هذا المثلث معلوم طولي ضلعين والمطلوب: إيجاد طول الضلع الثالثة ، عندئذ نستطيع استخدام نظرية فيثاغورث وذلك من خلال تطبيق الخطوات الآتية:
الخطوة 1:
نكتب نص نظرية فيثاغورث
الخطوة2:
نعوّض الوتر والضلعين القائمين بنص نظرية فيثاغورث أي نعوّض أضلاع المثلث القائم بالشكل الآتي:
ثمّ نعوّض أضلاع المثلث المعلومة والمجهولة بالوتر بالقاعدة السابقة.
نربع الأرقام فتتحول نظرية فيثاغورث إلى معادلة نحلها وذلك بنقل المجاهيل إلى طرف والمعاليم إلى طرف مع تغيير إشارة الحد المنقول، ثمّ نوجد جذر العدد المجهول فتنتج الإجابة المطلوبة.
أمثلة:
مثال1:
ABC مثلث قائم الزاوية في A
فيه:
AB=4 ،AC=3
المطلوب:
أوجد طول الضلع BC
الحل:
بما انّ المثلث قائم فيه ضلعين معلومين وضلع مجهول إذاً نستطيع تطبيق نظرية فيثاغورث.
نكتب نص النظرية:
مربع الوتر يساوي مجموع مربعي الضلعين القائمين
نعوّض بالأضلاع:
نعوّض بالأرقام المعلومة:
نربع ونجمع:
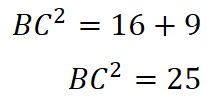
نجذر الطرفين:
BC=5
وهو المطلوب
مثال2:
ABC مثلث قائم في B
فيه:
AB=8، AC=10
والمطلوب: أوجد طول BC
الحل:
نطبّق نفس الخطوات السابقة:
مربع الوتر يساوي مجموع مربعي الضلعين القائمين
ننقل المجاهيل إلى طرف والمعاليم إلى طرف مع تغيير اشارة الحد المنقول فينتج:
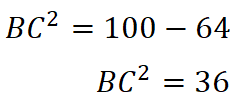
نجذر الطرفين:
BC=6
وهو الناتج المطلوب.